This is an article for kids explaining how GPS location through phones works. There is also an activity that kids can do after reading through this article. (The activity will be coming soon)
Background
Have you ever wondered how emergency responders can locate a mobile phone? Or how GPS can tell you your location, to within a few feet? We won't go into all of the details of the technology, but because the phone or GPS communicates with towers or satellites whose locations are known, it is possible to determine the location of the device.
First let's think about cell phones. Whenever you make a call on a cell phone, the signal goes to a nearby antenna on a tower, called a base station. (This is similar to the way a cordless phone transmits a signal to a base within a house.) From the base station, the signal is transmitted through the network to the other phone. The coverage is determined by the location of the antennas, with each antenna communicating to nearby mobile phones within a "cell."
The following diagram from Wikimedia commons (public domain) shows hexagonal cells.
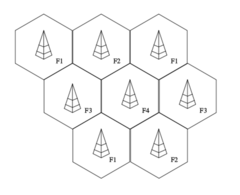
This figure shows a network with neighboring cells transmitting with different frequencies. We can think of each tower communicating with all mobile phones within its cells, but the number of calls that one tower can handle has an upper limit. What if there are too many calls in one cell? One solution is to divide up a cell into smaller cells and use more towers. If you look at a map of cell tower locations, they are not on an even grid, but may be concentrated around highways or heavily populated areas, or wherever the network provider has permission to put a tower with an antenna! But it is important to realize that the cell boundaries are not real boundaries. While the signal will be stronger from a phone to a nearby tower, it is still possible to communicate with towers that are farther away.
In the US, the FCC (Federal Communications Commission) requires cell phone companies to include a way to locate cell phones, for rescue workers and 911 service. Depending on the type of phone, there are different ways that it could be located. Even with older phones, if a phone is within range of one tower, then we know it is somewhere within the "coverage" of that tower. If the phone is in range of 2 towers, we know the phone is in the intersection of the two coverage areas. Whenever a cell phone is turned on, it is continually broadcasting signals or messages which base stations are monitoring. These messages are required in case someone else wants to call your cell phone. This means that the location of a cell phone can be found without even being on a call.
With newer phones, it is possible to estimate the range (distance) or angle between the tower and the phone, by measuring delays between towers receiving the same message from the same phone. Also, more phones now include a GPS receiver to determine location, which also uses range information; we'll discuss GPS later. Cell phone technology varies and is updated over time, but the basic principles of geometry using range information is where we'll focus today.
How can we use range information to determine location? Suppose someone is driving along a straight road, and the car and the tower are on the same road. If we know the location of the tower A and the range to tower A, there are 2 possible locations for the car, as shown below.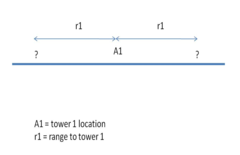
Along a line, it takes 2 ranges to locate the car unambiguously.
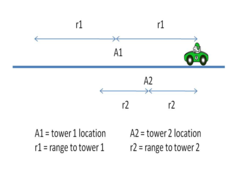
On the other hand, if the car is in a parking lot (on a plane), knowing the range from a fixed position narrows the possible location to a circle in the plane. If the range is known to 2 reference points, there are 2 possible locations for the car. If we know the range to a 3rd reference point, we have enough information to tell the location (assuming the reference points are not in a line).
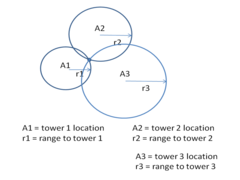 Finding the location using three ranges is called "trilateration." Another common term is "triangulation," although triangulation can mean determining location from three angles. The location of a cell phone gives important information to emergency responders, and is also useful for criminal investigations.
Finding the location using three ranges is called "trilateration." Another common term is "triangulation," although triangulation can mean determining location from three angles. The location of a cell phone gives important information to emergency responders, and is also useful for criminal investigations.
Can you think of other ways that trilateration or triangulation could be used? When making a sketch of a crime scene, the preciselocation of evidence is important. A crime scene investigator will take pictures of the scene, and also measure distances between evidence and fixed objects. For instance, if a weapon is found on the floor, two distances are measured, often either the perpendicular distance to 2 walls, or distances to 2 room corners. Why only 2 distances instead of 3? Even though two ranges gives 2 possible locations, only one location would be inside the room - the other would be outside. The room walls provide the extra information needed.
Today we will do an exercise where we will use a compass and find the intersection of circles to locate objects on a sketch. Note that we have simplified our examples, by disregarding the height of objects, but with math we are able to obtain a numerical solution.
But before that, let's talk about GPS. The same geometry applies, except that height is definitely not negligible, so we have added another dimension to the problem. GPS stands for Global Positioning System. There are about 32 satellites orbiting the Earth (more launches are planned) and each one broadcasts a message every 30 seconds that tells the exact time and position of the satellite. These messages travel at the speed of light, but there is a measurable delay when the message is received; the receiver is also synchronized to atomic time. Since the distance is the speed of light multiplied by the message delay, the range to a satellite can be computed. In 3D, knowing the range to one satellite narrows the possible locations to the surface of a sphere. The GPS receiver receives messages from multiple satellites, so if 2 satellites ranges are known, that narrows the location to the intersection of 2 spheres, which is a circle. [Image used for camp by permission]

Then can you guess how many satellite ranges are needed for GPS? The range to a 3rd satellite narrows the location to 2 positions, and a 4th satellite range will indicate which position is the true location. Sometimes 3 satellites is accurate enough, if only one of the two positions is on the Earth's surface.
Finally, some of you may be wondering how it is possible to measure time so accurately. International Atomic Time is found by averaging the time of 200 atomic clocks in about 70 national laboratories worldwide. Each of the labs broadcasts its time, and the times are compared using satellites. Time signals from atomic clocks are broadcast over radio signals by several governments, which can be received in most places of the world [Wikipedia: International Atomic Time, atomic clock]. By the way, if you purchase an "atomic clock" at the store, it is really a clock that gets its time over radio from a government atomic clock.
So you see that range is very useful information. We could go on and on, and talk about things like laser distance measuring devices (much faster and more accurate than measuring tape), and range cameras that can produce 3D face images, for 3D face recognition. But the application that we'll focus on today is the location of cell phones or crime scene objects, using trilateration, a.k.a. triangulation.
















What other people said
Average Rating (0)
Log in or Join now to rate this article!